| Dokumente | |
|
|
Dokumentvorschau |
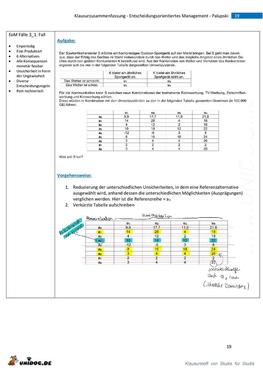
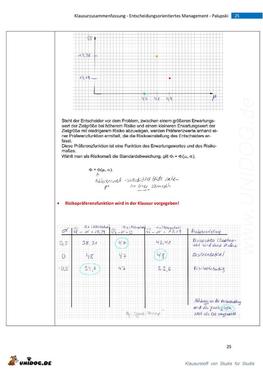
Klausurzusammenfassung_EoM_Entscheidungsorientiertes Management_FOM_DO_Palupski |
Dokument-Nr.: F-AMQV |


|
|
Dokument-DownloadUm Zugriff auf dieses Dokument zu erhalten, musst Du Mitglied der UNIDOG Community sein. |
|
Inhalt / Beschreibung
Klausurzusammenfassung zum Thema Entscheidungsorientiertes Management beim Prof. Palupski an der FOM in Dortmund. Die Zusammenfassung bezieht sich auf das Wintersemester 2018/2019. Das Skript von fast 300 Seiten habe ich für die Klausurvorbereitung auf 68 in tabellarischer Form zusammengefasst, sodass die einzelnen Themen wie ausführliche Vokabeln gelernt und wiederholt werden können. Folgende Inhalte könnt Ihr u.a. der ausführlichen Zusammenfassung entnehmen:
interpretieren
Ich wünsche euch viel Erfolg beim Lernen! Viele Grüße! Erreichte Klausurnote: 1,7 |
Dokumentbewertung (2)
Kommentare
Dokument empfehlen

|
||||||||||||||||
|
Vorschau-Ausschnitte
|
|||||||